By using
the sine formula on a triangle as follows:
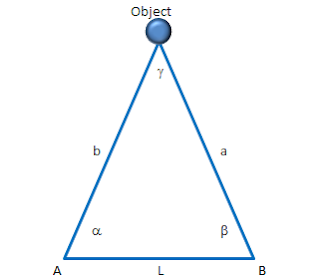
a / sin a = b / sin b = L / sin g
Where a and b is not necessarily equal or
should not an isosceles triangle. And g can be determined as follow:
180o – a – b – g = 0o
g = 180o –
a – b
Picture a
triangle above is considered as a top view of a plan to measure
the distance from A to objects or measure the distance from
B to object.
If
the angle a is known, the distance between
A to B or L is
known, and the angle b is known, then the
distance between A to object, and the distance between B to object can be calculated, without the need to go
to the object directly.
The distance between A to object is:
B = sin b x L / sin b g = sin x L / sin (180 - a - b)
The distance between B to object is:
a = sin a x L / sin a g = sin x L / sin (180 - a - b)
If the distance between A to B or L is 50 meter, the angle is 55o and angle a b is 60o then:
Distance from A to object = b = sin 60 x 50 / Sin (180-55 -60) = 47.8 meters
Distance from B to object = a = sin 55 x 50 / Sin (180-55 -60) = 45.2 meters
Results with the best accuracy obtained if a and b are about 35 to 55 degrees. By using a Theodolite or Total Station equipment as used by the surveyors in the field of geodesy, the measurement can be performed with accuracy up to seconds.
Common angle measurements are in degrees, minutes, and seconds (DMS). One degree is equal to 60 minutes, and one minute is equal to 60 seconds. One rotation is 360 degrees.
This Excel sheet is containing the following formula to calculate
the distance to an object.
Unit of measurement
of distance that is calculated can be anything, such as: meters, km, feet, miles,
etc..
For angle
measurement, always use the degrees unit.
No comments:
Post a Comment
Your positive comment will be highly appreciated to improve this site